Los modelos matemáticos buscan describir sistemas reales, tanto naturales como artificiales, mediante el uso de un conjunto coherente de expresiones matemáticas. Existe una clasificación de los modelos matemáticos que los divide en modelos basados en mecanismos y modelos basados en datos. Como casi toda clasificación, en la realidad puede ser difícil encontrar ejemplos de estas clases en estado puro. Sin embargo, es posible decir, al menos de manera aproximada, que cada una de ellas lleva implícitas formas muy características de realizar descripciones de la realidad.
Los modelos basados en mecanismos parten de relaciones entre cantidades relevantes que describen procesos que ocurren en la realidad. Por ejemplo, desde la física del continuo, la conducción del calor se concibe como un flujo que se da desde los lugares más calientes a los más fríos de un cuerpo. Por lo general, este tipo de modelos usan ecuaciones diferenciales para describir los procesos de interés. Entonces, en la actualidad, para no tener la necesidad de recurrir a simplificaciones groseras, se suelen usar los llamados métodos numéricos para la resolución de dichas ecuaciones. Esto se puede hacer gracias a la existencia de computadores, los cuales permiten realizar gran cantidad de operaciones sencillas en tiempos muy cortos.
Por otro lado, los modelos basados en datos buscan encontrar relaciones entre variables de entrada y variables de salida mediante funciones que transforman las primeras en las segundas. En alguna medida, se trata de modelos de “caja negra” que no transparentan los procesos que están ocurriendo dentro del sistema estudiado. En la actualidad, un ejemplo relevante de este tipo de modelos son los basados en las llamadas redes neuronales artificiales. Estas se basan en una analogía con el funcionamiento de las neuronas y sus conectividades.
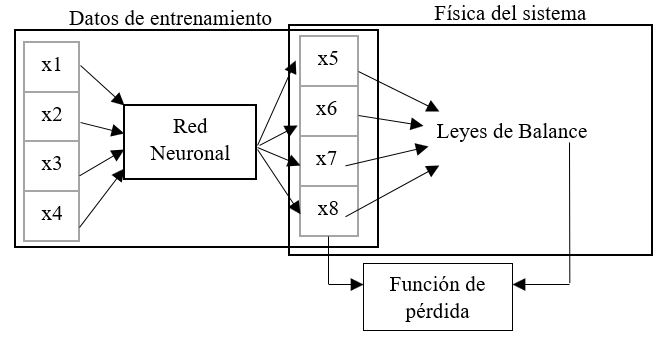
Recientemente, ha emergido una corriente de modelización que intenta reunir las virtudes de cada uno de los tipos de modelos descritos anteriormente. La idea es incluir información a priori sobre la física de los procesos que se quieren describir en la estructura de los modelos basados en datos. Por ejemplo, es posible imponer matemáticamente ciertas leyes de conservación (la conservación de la masa, por ejemplo) en la arquitectura de una red neuronal. De esta manera, se puede alimentar al modelo los datos recogidos mediante monitoreo y a la vez se puede asegurar que se cumplan las leyes de balance que se sabe que gobiernan el fenómeno analizado. De esta manera, se está apuntando a contar con las mejores características de los dos grandes paradigmas de modelización matemática.
Sobre autor/a
Esteban Samaniego
Ingeniero civil por la Universidad de Cuenca. Tiene un doctorado por la Universidad Politécnica de Cataluña. En la actualidad es profesor titular principal en la Facultad de Ingeniería y el Departamento de Recursos Hídricos y Ciencias Ambientales de la Universidad de Cuenca.
Ingeniero civil por la Universidad de Cuenca. Tiene un doctorado por la Universidad Politécnica de Cataluña. En la actualidad es profesor titular principal en la Facultad de Ingeniería y el Departamento de Recursos Hídricos y Ciencias Ambientales de la Universidad de Cuenca.
Español
简体中文
English
Français
Deutsch
Ελληνικά
Italiano
日本語
Português
Русский